BISAC NAT010000 Ecology
BISAC NAT045050 Ecosystems & Habitats / Coastal Regions & Shorelines
BISAC NAT025000 Ecosystems & Habitats / Oceans & Seas
BISAC NAT045030 Ecosystems & Habitats / Polar Regions
BISAC SCI081000 Earth Sciences / Hydrology
BISAC SCI092000 Global Warming & Climate Change
BISAC SCI020000 Life Sciences / Ecology
BISAC SCI039000 Life Sciences / Marine Biology
BISAC SOC053000 Regional Studies
BISAC TEC060000 Marine & Naval
On the base of experimental data it was revealed that type of wave breaking depends on wave asymmetry against the vertical axis at wave breaking point. The asymmetry of waves is defined by spectral structure of waves: by the ratio between amplitudes of first and second nonlinear harmonics and by phase shift between them. The relative position of nonlinear harmonics is defined by a stage of nonlinear wave transformation and the direction of energy transfer between the first and second harmonics. The value of amplitude of the second nonlinear harmonic in comparing with first harmonic is significantly more in waves, breaking by spilling type, than in waves breaking by plunging type. The waves, breaking by plunging type, have the crest of second harmonic shifted forward to one of the first harmonic, so the waves have "saw-tooth" shape asymmetrical to vertical axis. In the waves, breaking by spilling type, the crests of harmonic coincides and these waves are symmetric against the vertical axis. It was found that limit height of breaking waves in empirical criteria depends on type of wave breaking, spectral peak period and a relation between wave energy of main and second nonlinear wave harmonics. It also depends on surf similarity parameter defining conditions of nonlinear wave transformations above inclined bottom.
emecs, sea coasts, wave breaking, spilling, plunging, limit height of breaking waves, surf similarity parameter, spectral structure of waves.

Numerous laboratory and field experimental data demonstrate high variability of testify the wide range of changes of  in a breaking point: from 0.4 up to 1.2. These variations, as well as various types of a breaking of waves, can be explained with distinctions of the amplitude-phase frequency structure of waves before a breaking. The highest nonlinear wave harmonics, arising due to near resonant triad interactions, periodically exchange of energy with the main harmonic. A phase shifts between them also periodically fluctuate due to nonlinear and dispersive effects. The changes of phases and amplitudes of the highest nonlinear wave harmonics during transformation of waves lead to increasing of acceleration of water particles in a crest of waves greater, than acceleration of gravity, or orbital velocities in a wave crest becomes higher than the phase celerity of waves that will cause a wave breaking. Changes of phases and amplitudes of the highest harmonics depend on prehistory of wave transformation, because many combinations of phases and amplitudes of harmonics of different frequencies can be observed. It provides a variability of type of breaking of waves and a wide range of ratios between height of a wave and water depth in a breaking point.
in a breaking point: from 0.4 up to 1.2. These variations, as well as various types of a breaking of waves, can be explained with distinctions of the amplitude-phase frequency structure of waves before a breaking. The highest nonlinear wave harmonics, arising due to near resonant triad interactions, periodically exchange of energy with the main harmonic. A phase shifts between them also periodically fluctuate due to nonlinear and dispersive effects. The changes of phases and amplitudes of the highest nonlinear wave harmonics during transformation of waves lead to increasing of acceleration of water particles in a crest of waves greater, than acceleration of gravity, or orbital velocities in a wave crest becomes higher than the phase celerity of waves that will cause a wave breaking. Changes of phases and amplitudes of the highest harmonics depend on prehistory of wave transformation, because many combinations of phases and amplitudes of harmonics of different frequencies can be observed. It provides a variability of type of breaking of waves and a wide range of ratios between height of a wave and water depth in a breaking point.
The main purpose of this work is to find out the features of spectral structure of the waves breaking by spilling and plunging types and to investigate how it can influence on simple empirical criteria .
.
The data of two laboratory, one field and one numerical experiments performed by authors were used. A field experiment was performed at special research pier located on the Bulgarian coast of Black Sea near Shkorpilovtsy [6,7]. Wave data were registered by 15 wire string wave gauges, placed equidistantly at depth range from 0.5 to 4 m as shown at Fig.1b. Wave measurements in all 15 points were made simultaneously with a sampling frequency of 5 Hz and time duration of data series from 20 min up to 1 hour.
Two laboratory experiments were carried out in the wave flume of Research Center "Sea Coasts" in Sochi, Russia. Length of the flume is 22 m, width - 0.8 m, depth - 1 m. In the first experiment initially monochromatic waves with different amplitudes and periods propagate above underwater bar of forward slope 0.06, as shown at Fig. 1a. Waves were measured synchronously by 8 capacity type wire gauges. Duration of each run of measurements was from 1 up to 3 min with sampling frequency 200 Hz [5]. In second experiment different monochromatic waves were propagated above inclined bottom with mean slopes 0.043 and 0.022. Waves were registered by 15 wire capacity gauges. Duration of each run was from 1 up to 4 min and sampling frequency 50 Hz (Saprykina et al., 2015). At the end of flume waves were absorbed by a special constructed wave absorber and part of energy of reflected waves from the end of flume was less than 5%. For both experiments the water depth at the beginning of the slopes was 0.6 m. The depth at the top of bars was about 0.2 m. In field and laboratory experiments breaking type was defined visually and fixed by video and photo images.
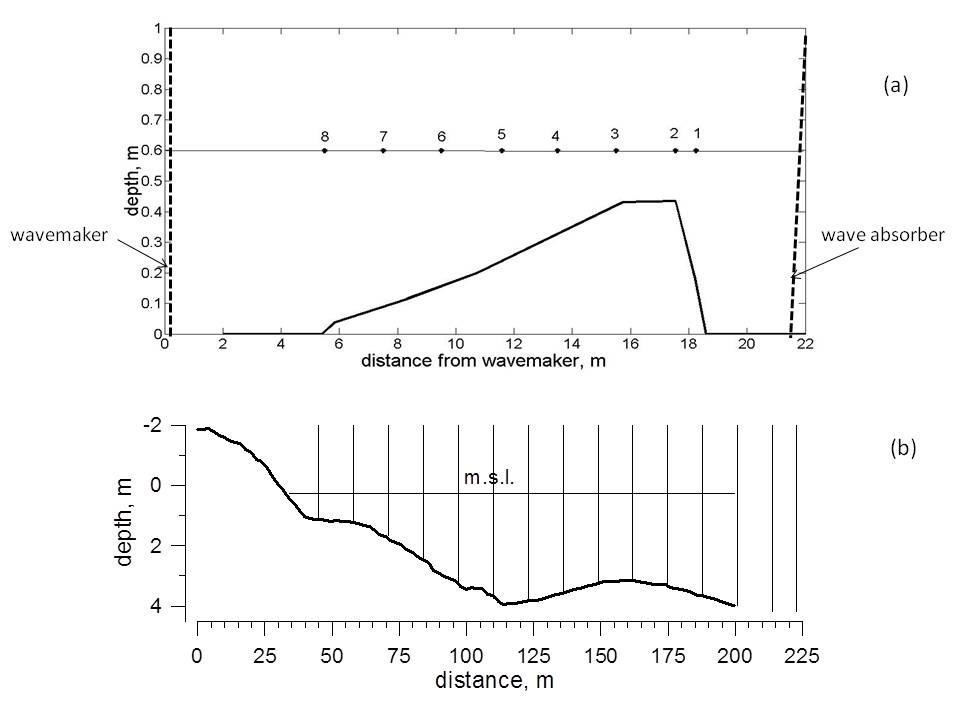
Fig 1. Setup of laboratory experiment
Numerical modeling was performed using MIKE 21 BW developed by DHL and based on Boussinesq type equations. The wave breaking is described on the base of roller conception suggested in [3] and, as it was proved in many investigations, is suitable for spilling and plunging types of wave breaking [4]. The influence of type of wave breaking on limit height of irregular breaking waves (2) was studied. Numerical wave flume had the length 1000 m, depth linearly decreasing toward to the shore in the manner to corresponding initial water depth that was 10, 15, 20, 30 and 40 m, that required the bottom slopes 0.01, 0.015, 0.02, 0.03 and 0.04 respectively. To receive different types of wave breaking (Sp and Pl) the initial wave heights of range 0.4 – 1.1 was used. A set-up and run-up of waves on the coast was not taken in account. At the modeling absorbing boundary conditions was applied. Initial waves (a time series of free surface elevations) were irregular and generated from JONSWAP spectrum (peak parameter 3.3) with random distributed phases on [0, π]. Type of wave breaking was defined by parameter of surf similarity (1). According [9], we associated a moment of beginning of wave breaking with a maximum of a radiation stress. A point, where there was the maximum of radiation stress and the minimum of mean water level was a sign of the beginning of wave breaking. For this point local significant wave height Hb and local water depth were calculated. Total 54 runs of numerical experiments were performed; duration of wave records - 25 min.
III. Spectral structure of plunging and spilling breaking waves
Laboratory experiments
As typical example of Sp and Pl breaking waves we will consider the series of measurements 48 and 49 where the waves propagate over the forward slope 0.043 and break at the end of forward slope or on the top of the bar. The parameters of waves are shown at Tab. 2.
Table 2. Wave parameters in experiment
|
Run |
Wave height, m |
Wave period, s |
Type and location of wave breaking |
|
48 |
0.14 |
2.29 |
Spilling, 18.5 m |
|
49 |
0.15 |
2.03 |
Plunging, 17 m |
Spatial evolution of asymmetry of waves, local wave steepness and the relative height of waves are shown in Fig. 2. It is visible that the waves breaking of Pl type are asymmetric on vertical axis (asymmetry coefficient As is negative), i.e. they have the steep forward front, while the waves breaking by Sp type – symmetric (asymmetry is about zero). The breaking occurs approximately at the same local relative height of a wave - H/h=0.78 that corresponds to usual criteria of limit depth of wave breaking.
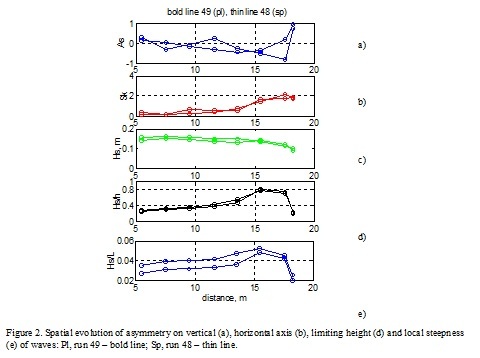
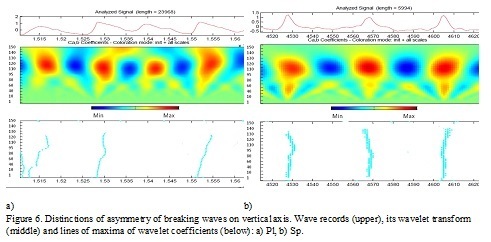
To find out the details of distinctions in asymmetry of waves, the wavelet analysis was applied (Fig. 3). The first harmonic of waves corresponds to frequency 0.44 Hz, the second harmonic – 0.88 Hz, and 0.49 Hz, 0.98 Hz for runs 48 and 49 respectively. The values of wavelet coefficients are shown by intensity of color. It is obvious that symmetry of waves is connected with a relative location in crests of the first and second harmonics of waves. At the breaking by Sp type, maxima (crests of waves) of the second harmonic coincide on time with crests of the first one that is confirmed by a vertical lines of maxima (Fig. 3, a). At a breaking by Pl type the second harmonic are shifted on time relatively the first forward (Fig. 3, b).
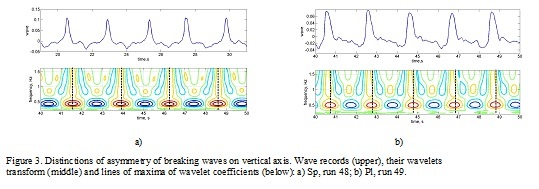
The differences of phase structure of waves can be explained by a different stage of their transformation before a breaking depending on a periodic exchange of energy between the first and second nonlinear harmonics. At Fig. 4 the evolution of amplitudes of the first and second harmonics of waves during transformation in flume are shown. In run 48 the second harmonic before a breaking had high amplitude, there was a backward transfer of energy from the second harmonic to the first one and dispersive processes prevailed over nonlinear that lead to shift of the second harmonic back and to formation of a symmetric wave before a breaking. In run 49, second harmonic before a breaking growing, nonlinear processes of transformation of waves prevailed and the second harmonic is displaced forward, forming a "saw-tooth" type wave with the steep forward front. Results of laboratory experiment are confirmed in field conditions
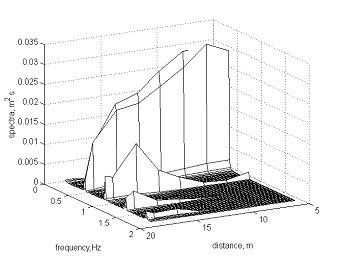
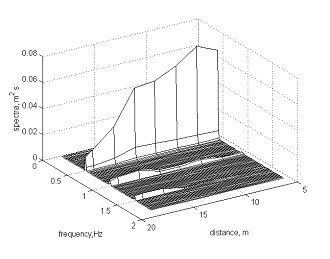
.Fig 4. Evolution of wave spectra: a) Sp, run 48, b) Pl, run 49.
Field experiment
Let consider distinctions of the amplitude-phase frequency structure of waves breaking by Sp and by Pl on the example of a run 36 - swell waves with the peak period about 7 seconds and narrow spectrum. The evolution of wave spectra and wave energy in frequency band of first and second nonlinear harmonics are shown on figure 6. For these waves the scenario of transformation of waves with a periodical in space exchange of energy between first and second harmonics is typical [8] and therefore two lines of wave breaking exist. In outer surf zone waves breaking as Sp type, and in inner – as Pl type (Fig. 5).
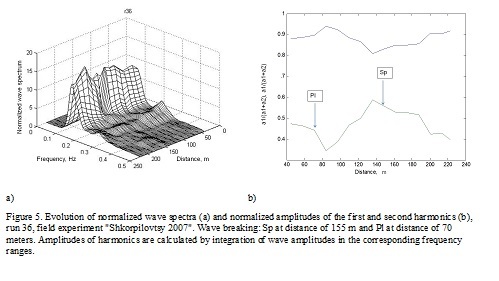
In process of propagation of deep water waves to intermediate depth (distance of 220 m) the second harmonic begin to grow (Fig. 5). Nonlinearity and dispersion processes approximately counterbalance each other therefore waves remain symmetric with respect to the vertical axis (Fig. 5) and break by Sp type on distance 155 m from the shore. At distance about 100 m, the second harmonic completely return their energy back to the first one and then again starts to grow. Dispersion of waves at this depth is relatively weak than nonlinearity and therefore the crest of wave of the second harmonic all the time is forward of a crest of the first, it leads to formation of a "saw-tooth" wave and its breaking by Pl type.
Asymmetry of waves and relative positions of harmonics are shown on Fig. 6. It is clear visible that the waves breaking by Pl type are close to "saw-tooth" shape and have the steep forward front, and waves breaking by Sp type have a sharp crest and a flat trough and are symmetric with respect to vertical axis that is confirmed by inclined lines of maxima for the Pl type breaking and vertical ones for Sp type breaking. Similar regularities are observed in other runs of experiment "Shkorpilovtsy 2007".
IV. Dependence of limit height of wave breaking on wave parameters and type of breaking
Laboratory experiments
The variations of limit height of breaking waves  (2) was analyzed on the data of laboratory experiment where initially monochromatic waves are propagate over inclined bottom with different slopes: 0.043 (steep) and 0.022 (gentle). Practically all breaking waves were of spilling type. Only one event of plunging breaking was observed. On figures discussed below to this events corresponds highest value of
(2) was analyzed on the data of laboratory experiment where initially monochromatic waves are propagate over inclined bottom with different slopes: 0.043 (steep) and 0.022 (gentle). Practically all breaking waves were of spilling type. Only one event of plunging breaking was observed. On figures discussed below to this events corresponds highest value of
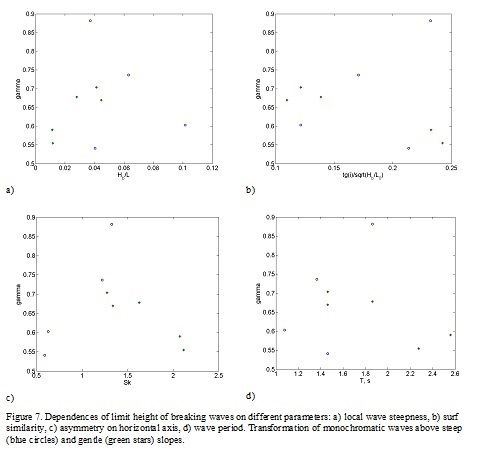
On Fig.7 the dependences of limit height of breaking waves on different parameters for waves transforming above steep and gentle slope are shown.
The limit height of breaking waves depends on steepness of breaking waves: it increases with increasing of wave steepness for waves with steepness less 0.05 and decreases for waves with steepness more 0.05. The limit height of breaking waves also depends on surf similarity parameters: it increases if parameter of surf similarity is less than 0.15
Numerical modeling experiments
For specification of the dependences received in the previous section numerical experiments were made.
On Fig.8 dependences of limit height of breaking waves on different parameters and type of wave breaking are shown. It is visible that limit height of irregular breaking waves in simple empirical criteria (2) depends on: a) spectral peak period; b) parameter of surf similarity; c) relation between wave energy of main wave harmonic and second nonlinear wave harmonic.
In general values of limit height of breaking waves for plunging waves are greater than for spilling waves. For plunging breaking waves a part of wave energy of second wave harmonics is lower than for spilling waves. This is connected with different spectral structure of waves and corresponds to laboratory investigations. The limit height of breaking waves for plunging waves decreases with increasing of energy of second wave harmonic, but for spilling breaking waves - increases.
Spilling breaking is typical for more short waves than plunging breaking. The limit height of breaking waves increases with increasing of wave period for spilling breaking waves. For plunging breaking waves it slightly decreases for wave periods from 10 up to 14 and increase for wave periods more 14 s. Plunging breaking occurs on more steeper slopes and near the coast line, but spilling breaking can occurs at greater distances from the coast due to differences of its spectral structure at nonlinear wave transformation.
The limit height of breaking waves for spilling waves has a linear dependence on surf similarity parameter at.
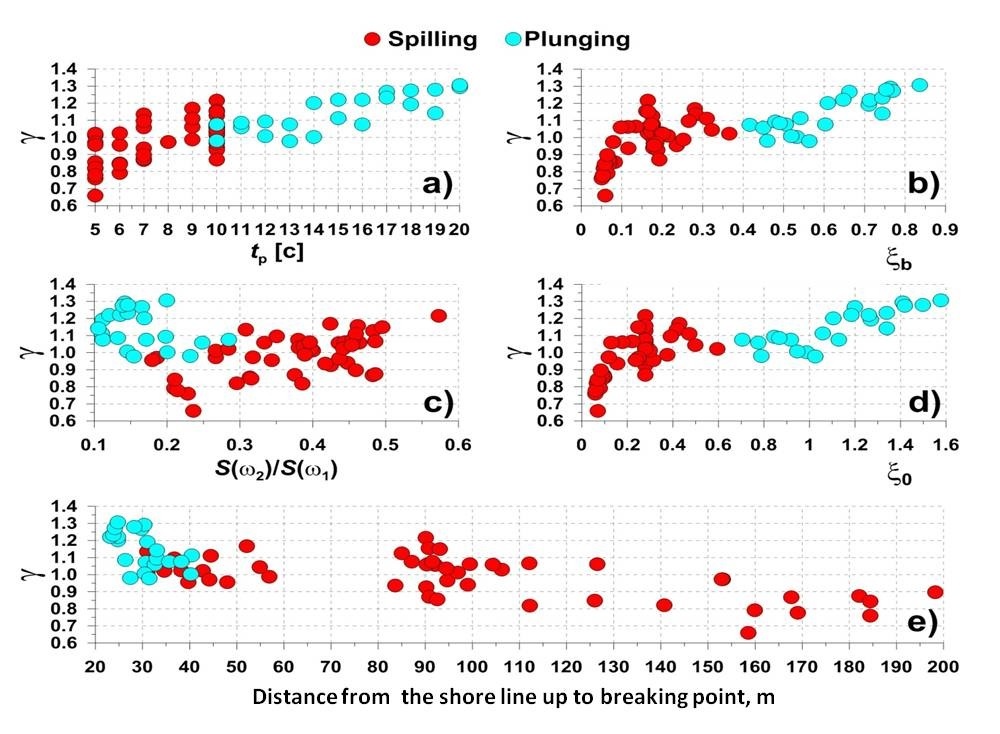
Fig 8. Dependences of limit height of breaking waves on on different parameters: a) wave period, b) d) surf similarity, c) on relative wave energy of second nonlinear harmonic, e) wave period distance from shoreline.
V. Conclusions
It was revealed that a type of wave breaking depends on wave asymmetry against the vertical axis at wave breaking point. The asymmetry of waves is defined by spectral structure of waves: a relative position in a crest of waves of the first and highest nonlinear harmonics, i.e. the ratio between amplitudes of first and second nonlinear harmonics and a phase shift between them. The relative position of nonlinear harmonics is defined by a ratio of the nonlinear and dispersive processes depending on a stage of nonlinear wave transformation and on the direction of energy transfer between the first and second harmonics. The value of amplitude of the second harmonic in comparing with first harmonic is significantly more in waves, breaking by spilling type, than in waves breaking by plunging type. The waves, breaking by plunging type, have the crest of second harmonic shifted forward to one of the first harmonic, so the waves have "saw-tooth" shape asymmetrical to vertical axis. In the waves, breaking by spilling type, the crests of harmonic coincides and these waves are symmetric against the vertical axis.
It was revealed that limit height of breaking waves in empirical criteria depends on type of wave breaking, spectral peak period and a relation between wave energy of main and second nonlinear wave harmonics, which are defined by spectral structure of waves. It also depends on surf similarity parameter defining on conditions of nonlinear wave transformations over inclined bottom.
VI. Acknowledgements
This work was supported by the Russian Foundation for Basic Research (project 14-05-00696) in frame of numerical modeling and by Russian Science Foundation (project 14-50-00095) in frame on physical modeling.
1. Battjes J. 1974. Surf similarity. Proc. 14th Conference Coastal Engineering (Copenhagen). New York, ASCE, pp. 466-480.
2. Battjes J.A., J.P.F.M. Janssen, 1978. Energy loss and set-up due to breaking of random waves. Proc. of XXVI Int. Coastal. Eng. Conf., p.p. 569-587.
3. Madsen A., Sorensen O., Shaffer H. 1997. Surf zone dynamics simulated by Boussinesq type model. Part I. Model description and cross-shore motion of regular waves. Coastal Engineering, 32, pp. 255-287.
4. MIKE21 BW - Boussinesq Waves Module. User Guide. http://www.hydroasia.org/jahia/webdav/site/hydroasia/shared/Document_public/Project/Manuals/WRS/MIKE21_BW.pdf
5. Kuznetsov, S., Ya.Saprykina . 2009 Mechanism of formation of secondary waves in coastal zone. Proceedings of International Conference on Coastal Dynamics 2009 “Impact of Human Activities on Dynamic coastal processes”, Tokyo, Japan, paper 9, ed. by M.Mizuguchi and S.Sato, World scientific.
6. Saprykina Ya.V., S.Yu. Kuznetsov, Zh. Cherneva, N. Andreeva, 2009, Spatio-temporal variability of the amplitude-phase structure of storm waves in the coastal zone of the sea, Oceanology, Vol. 49, No. 2, pp. 198-208.
7. Saprykina, Ya.V., S.Yu. Kuznetsov, H. Andreeva, M.N.Shtremel, 2013. Scenarios of nonlinear wave transformation in coastal zone, Oceanology, V.53, № 4, p.p. 422-431.
8. Saprykina, Y.V., Kuznetsov, S.Y., Kovalenko, A.N., 2015.Experimental studies of the local reflection of long waves from an underwater slope. Oceanology, 55 (2), pp. 171-181.
9. Stive M.J.F., H.G. Wind., 1982. A study of radiation stress and set-up in the nearshore region. Coastal Engineering, 6 , pp. 1-25..







