BISAC NAT010000 Ecology
BISAC NAT045050 Ecosystems & Habitats / Coastal Regions & Shorelines
BISAC NAT025000 Ecosystems & Habitats / Oceans & Seas
BISAC NAT045030 Ecosystems & Habitats / Polar Regions
BISAC SCI081000 Earth Sciences / Hydrology
BISAC SCI092000 Global Warming & Climate Change
BISAC SCI020000 Life Sciences / Ecology
BISAC SCI039000 Life Sciences / Marine Biology
BISAC SOC053000 Regional Studies
BISAC TEC060000 Marine & Naval
Arctic coastal systems are very sensitive to the freshwater budget mainly formed by river runoff. Great biases in estimation of total river runoff load to the Arctic Ocean proposed by the number of various scientific groups and insufficiency of physically-based, short-term, spatially diverse runoff predictions lead to strong necessity of state-of-art hydrological techniques implementation. At the moment the most powerful tools for the land hydrological cycle modeling are physically-based, conceptual or data-driven models. Better model – wider sources of hydrometeorological and landscape-related information we need to use to perform robust calculations. Severe climatic conditions of Arctic coastal region have led to weak river runoff monitoring net and a high level of uncertainties related to difficulties of direct measurements. There is the reason we need to develop modern techniques that allow providing effective runoff predictions by state-of-art models in the case of strong research data scarcity (for ungauged basins). Early stage of research aimed to coupling of conceptual hydrological model, cutting edge machine learning techniques and various sources of geographical data will be proposed with the call for intensification of cross-disciplinary research activities for the Arctic region sustainable development and safety.
arctic, runoff, modeling, ungauged basins, machine learning, SWAP
I. INTRODUCTION
A large part of the world rivers are ungauged in terms of ability to make accurate runoff calculations and predictions [8]. This problem is especially relevant for the Arctic region because of inability to estimate modern state of highly sensitive Arctic coastal ecosystems without high-resolution and well-proved river runoff calculations provided not only for the main large rivers, but also for small and mid-range rivers which usually have neither hydrological nor meteorological observations in their watersheds. Fig. 1 shows hydrologically ungauged area (there are no direct runoff measurement at all) of the Russian Arctic region. At first sight presented area is relatively small, but at the same time it takes the entire coastal zone of the Russian Arctic region. From this point it follows that the contribution of this coastal part to overall river runoff may be inconsiderable, but this tiny water budget plays important role for coastal zone ecosystems evolution and local communities’ life.
At the moment there is no one daily runoff database of Russian Arctic rivers for modern period. All available datasets use the same information of river discharges provided by the Global Runoff Data Center (GRDC, Koblenz, Germany) [14] that have some limitations. Firstly, modern Russian Arctic-related data have only monthly resolution that insufficient for use in state-of-art daily hydrological modeling procedures, and secondly, most of the daily data relates to the period of the late Soviet Union and in most cases we have no data at all after years of 1991-1993 (Fig. 2). Thereby at the moment we still faced the strong need of valid daily hydrological data.
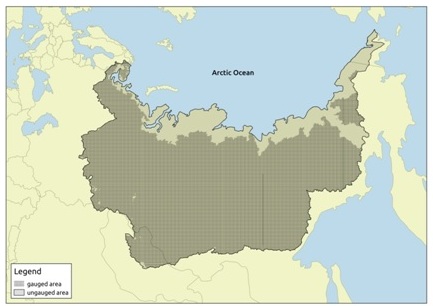
Fig. 1. Hydrologically ungauged (in space) area of the Russian Arctic region
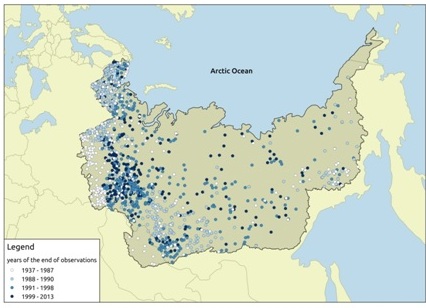
Fig. 2. Years of available river runoff data – hydrologically ungauged (in time) area of the Russian Arctic region (GRDC database)
Hydrological models are powerful, modern research tools for estimation of different features of water cycle processes. Despite of the type of hydrological model you choose (physically-based, conceptual or data-driven), the problem of determining model parameters will be acute [10, 11]. In the case of the basin under research have suitable direct runoff observations we can set up and solve a task of parameters estimation using calibration – model parameters obtaining procedure as an inverse task of runoff calculations. Implementing of hydrological models for runoff calculations in ungauged basins is a challenging task [13]. The set of methods aimed at finding the model parameters under insufficient hydrological data (fully or partially lack of direct runoff measurements), called regionalization [12]. There are numerous studies related to the problem of hydrological models parameters regionalization for ungauged basins, and typically it can be possible to divide methods presented in them into three main groups: based on physical similarity, based on spatial proximity and regression-based techniques [1, 12]. According to the analysis of more than 30 scientific articles related to the theme of regionalization, there is no universal approach to model parameters estimation for ungauged basins [2]. Thereby, runoff calculations for ungauged basins using highly data-dependent hydrological models require a comprehensive effort to a wide range of scientific issues from the model and its parameterization scheme identification to regionalization technique selection and source of hydrometeorological data we use.
II. DATA AND METHODS
Researched basins
The Nadym River, the Pur River, and the Taz River are one of the major rivers in the northern West Siberia; rivers flow through the territory of the Yamalo-Nenets Autonomous District of Russia and belong to the Kara Sea basin [7] (Fig. 3). All of researched basins are quite similar in geographical and hydrological conditions (Table 1).
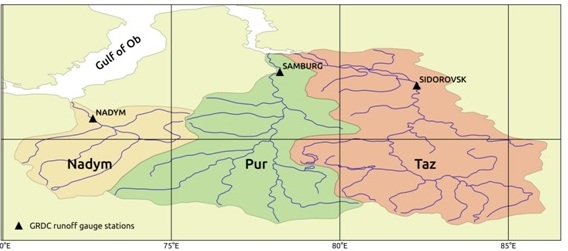
Fig. 3. Researched river basins
Table 1. Comparative characteristics of researched river basins
|
River |
Drainage area, km2 |
Length, km |
Mean runoff, mm/year |
|
Nadym |
64 000 |
545 |
290 |
|
Pur |
112 000 |
1024 |
293 |
|
Taz |
150 000 |
1401 |
305 |
Hydrological data
Observed daily runoff data of researched river basins at closest to the mouths gauges (Fig. 3) were obtained from GRDC database [14] under standard request. Runoff data length was unified for all rivers and contains period from 1979 to 1991 year. Modern data from these gauge stations are not freely available for scientific purpose and are not taken into consideration in this work. Runoff values were converted from m3/s to mm/day.
Meteorological data
Meteorological forcing data were obtained from WFDEI database [15] that based on ERA-Interim forcing product by the European Centre for Medium-Range Weather Forecasts (ECMWF). WFDEI database have the data of eight meteorological variables with daily time resolution and 0.5º x 0.5º spatial resolution with global land coverage. Temperature and bias-corrected by Climatic Research Unit (CRU) rainfall and snowfall precipitation rates were used as input forcing to conceptual hydrological model. In case of machine learning rainfall-runoff model implementation all available meteorological variables were used. Lumped implementation of developed rainfall-runoff models leads to the need of weighted averaging of all forcing variables across researched basins.
Conceptual hydrological model
In this study simplified conceptual, lumped hydrological model Hydrologiska Byråns Vattenbalansavdelning (HBV) [4] were used. Schematic diagram of processes represented by simplified HBV model is presented on the Fig. 4.
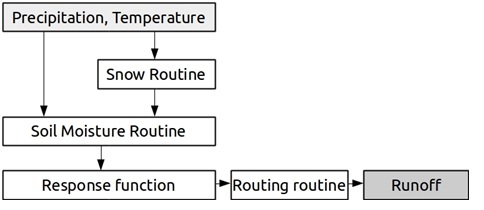
Fig. 4. Schematic structure of HBV model
During the last decades HBV model has been successfully used in numerous scientific studies and engineering tools all over the world. Traditionally HBV model was used to runoff calculations for small and medium sized basins (< 10 000 km2), but some researchers are attempting to generalize local results to macro (global) scale [3]. In presented study we will investigate the possibility of s-HBV model simulate river from large (> 50 000 km2) river watersheds.
Machine learning (data-driven) model
The increasing popularity in hydrological modeling methodology refers to modern data-driven (machine learning) techniques. Key concept of these methods – to set up robust relation between meteorological forcing data and runoff observations without any knowledge of specific geographical or hydrological patterns. In this study we implemented the most widely used solution for regression tasks – Decision Tree model. Typical Decision Tree is a "white box" consists of the range of boolean classifiers which split our samples to tiny "leaf" nodes where all samples constantly refers to the one target value (Fig. 5).
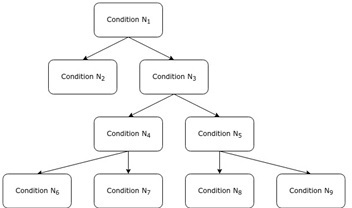
Fig. 5. Scheme of simple ordinary Decision Tree model
Single tree-based implementation of Decision Tree algorithm faced with the case of over-fitting and robustness lack that lead to limited using in real world examples. In our work we used cutting-edge machine learning technique based on ensemble approach to predictions: Random Forest Regression (RFR). RFR is based on ensembles of simple Decision Tree models and provide useful tricks such bagging and bootstrapping which totally reduce over-fitting and make our models suitable to provide robust predictions [5]. There are limited applications of RFR in daily river runoff modeling, but in [6] this technique has been successfully implemented for monthly runoff simulations across the Europe.
Modeling efficiency criterion
In presented study widely used and most-known for runoff modeling efficiency estimation criterion proposed by Nash and Sutcliffe (NS) [9] was used as follows:
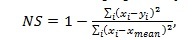
where xi , yi - observed and simulated runoff in i day, xmean - mean observed runoff.
III. RESULTS AND DISCUSSION
Case study 1: calculations for ungauged (in time) basins
The last year of observational data for all researched basins is the year of 1991 inclusively. It is a reason to refer these basins to “ungauged in time” group – there are no information of their current hydrological state history. To get robust estimates of current river runoff conditions, it is necessary to tune our hydrological model to data we have, i.e. to calibrate model parameters. Model parameters calibration has been carried out on entire observational period (1979-1991) in automatic manner with the use of standard Newton conjugate gradient (Newton-CG) algorithm implementation. Newton-CG is cost-efficient, multivariate function optimization algorithm typically used for local minimum search. In our study it showed comparative performance with algorithm of global optimization – differential evolution – wherein used less computational time. NS criterion (Eq. 1) was chosen as an objective function for calibration. Obtained optimal parameters are robust – up to 10 runs of Newton-CG optimization with different initial conditions showed the same results.
Further calculations of river runoff for entire researched period (1979-2014) were performed (Fig. 6).
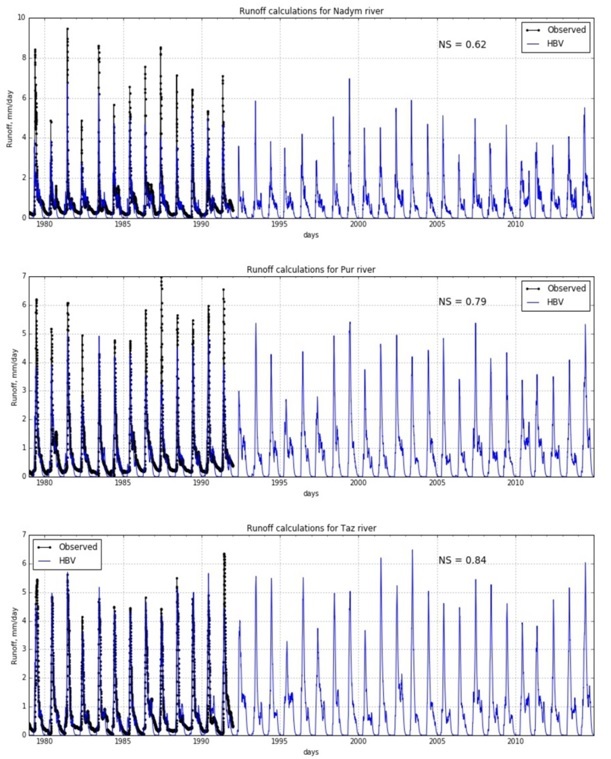
Fig. 6. Runoff modeling results
Obtained results show good performance of HBV model for runoff calculations for large Russian Arctic rivers. The larger river – the better modeling efficiency. We suppose that this fact corresponds with scale effect of runoff formation processes with one hand, and local basin features with another hand. For all researched basins significant underestimation of autumn-summer period runoff was noted. This effect is caused by HBV hydrological model structure simplification or by using rough estimates of monthly potential evaporation values which can overestimate evaporation potential of observed river basins. Obtained results have much in common with physically-based distributed SWAP model results provided in [7].
Case study 2: calculations for ungauged (in space) basins
In the case of observed runoff lack hydrologists often face with impossibility to provide model parameters calibration procedure. Then different parameters regionalization strategies will be implemented [1, 2, 12, 13]. The most intuitive way to set up model parameters for ungauged basins (and the most used for engineering applications) is regionalization based of spatial similarity which in practice is full transfer of model parameters set (derived by calibration or any other method) from gauged (or donor) to ungauged (or recipient) catchment. In this study we successively implemented all optimal parameters sets (derived for each river through calibration) for all rivers under research and estimated corresponding runoff modeling efficiency (Table 2).
Table 2. Runoff modeling efficiency (NS) with various sets of parameters
|
River |
Optimal set of parameters |
||
|
Nadym |
Pur |
Taz |
|
|
Nadym |
0.62 |
0.41 |
0.37 |
|
Pur |
0.38 |
0.79 |
0.75 |
|
Taz |
0.57 |
0.84 |
0.84 |
Obtained results show significant modeling efficiency reduction for Nadym River in case of using parameters sets both from Pur and Taz rivers. Further results show that optimal parameters set of HBV model for Nadym River by itself has moderate performance not only for runoff modeling routine, but for regionalization procedure too – efficiency reduction has significant value for both Pur and Taz rivers in case of calculations based on optimal parameters for Nadym River. The best results were obtained for Pur and Taz rivers tandem. For Taz River we have no modeling efficiency reduction using Pur River optimal parameters at all, and for Pur River we have insignificant efficiency reduction.
Finally we suppose that Pur River optimal HBV model parameters are appropriate choice for initial conditions set up or a priori parameters set for river basins in similar geographical conditions.
Machine learning technique implementation for runoff post-processing
Simplified HBV model which was implemented in this study provides good daily estimations of river runoff in terms of Nash-Sutcliffe efficiency criterion, but despite this, modeled runoff time-series has similar faults end error in similar water regime phases: in the spring flood HBV model underestimates absolute value of runoff peak, and usually underestimates baseflow in the summer-autumn period. The main idea of machine learning technique implementation in this case consists in hypothesis that all observed HBV model errors have non-random reasons and can be described using complex statistical model such as RFR.
For checking this hypothesis post-processing of modeled runoff time-series based on cutting-edge machine learning algorithm (RFR) was implemented in cross-validation manner: for train period we reserved all available years except one year which related to test period. Input data (feature matrix) for RFR were constructed by meteorological forcing data and HBV modeled runoff output. Residuals between observed and modeled runoff were chosen as output target labels. Thereby for each researched year and river we independently implemented coupled system of conceptual HBV model provided physically-based runoff calculations with machine learning post-processing approach based on RFR model (HBV-ML) and received the results of runoff modeling efficiency for both HBV and HBV-ML models (Fig. 7).
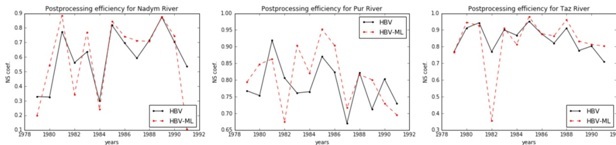
Fig. 7. Cross-validation results for ordinary conceptual model efficiency (HBV) and coupled system of conceptual model and machine learning post-processing technique (HBV-ML)
The results show uncertain efficiency improvements of machine learning based post-processing implementation to modeled runoff. On the average there is no such NS growth for all researched basins, i.e. positive results compensate with negative results of provided post-processing. For the Nadym River provided technique showed better results for 7 of 13 years, for the Pur River – for 8 of 13 years, and for the Taz River – for 9 of 13 years. Further research of provided novel post-processing approach limitations is needed.
Despite of well-proved machine learning models efficiency for decision making in many technological-oriented industries, they face serious limitations and provide significant discrepancies (uncertainties) in actual hydrological case studies. Understanding of runoff formation mechanisms, hydrological processes description and deeper implementation of this knowledge in community mathematical models are still the best way to improve runoff calculations (especially for ungauged basins in permafrost regions) rather than adaption of complex statistical (machine learning) models for modeled river runoff post-processing purposes.
IV. ACKNOWLEDGMENTS
The part of the studies related to mining and analyses of hydrometeorological data, developing data-driven models and runoff calculations for ungauged basins was funded by the Russian Foundation for Basic Research (RFBR) according to the research project № 16-35-00159 mol_a. The part of presented studies related to the developing, adapting and implementing of conceptual hydrological model was financially supported by the Russian Science Foundation (grant № 16-17-10039). The part of the studies related to post-processing efficiency estimation was supported by the Russian Ministry of Education and Science (grant № 14.B25.31.0026).
The present work has been carried out within the framework of the Panta Rhei Research Initiative of the International Association of Hydrological Sciences (IAHS).
1. G. Ayzel, “Artificial Neural Network Technique Implementation for the Hydrological Model Parameters Search”, Russian Scientific Journal, 2014, vol. 40, no. 2, pp. 282-287 (In Russian).
2. G. Ayzel, “River Runoff Calculations for Ungauged Basins: the Potential of Using Hydrological Model and Artificial Neural Network Technique”, Engineering Surveys, 2014, no. 7, pp. 60-66 (In Russian).
3. H. Beck et. al., “Global-Scale Regionalization of Hydrologic Model Parameters”, Water Resources Research, 2016 (in press).
4. S. Bergström, Development and Application of a Conceptual Runoff Model for Scandinavian Catchments. Norrköping: SMHI RHO 7, 1976. 134 p.
5. L. Breiman, “Random Forests”, Machine learning, 2001, vol. 45, no. 1, pp. 5-32.
6. L. Gudmundsson, S. Seneviratne, “Observational Gridded Runoff Estimates for Europe (E-RUN version 1.0)”, Earth Syst. Sci. Data Discuss., 2016 (in press).
7. E. Gusev, O. Nasonova, L. Dzhogan, G. Ayzel, “Simulating the Formation of River Runoff and Snow Cover in the Northern West Siberia”, Water Resources, 2015, vol. 42, no.4, pp. 460-467.
8. M. Hrachowitz et al., “A Decade of Predictions in Ungauged Basins (PUB) - a Review”, Hydrological Sciences Journal, 2013, vol. 58, no. 6, pp. 1198-1255.
9. J. Nash, J. Sutcliffe, “River Flow Forecasting Through Conceptual Models Part I - A Discussion of Principles”, Journal of hydrology, 1970, vol. 10, no. 3, pp. 282-290.
10. O. Nasonova, E. Gusev, G. Ayzel, “Optimizing Land Surface Parameters for Simulating River Runoff from 323 MOPEX-watersheds”, Water Resources, 2015, vol. 42, no. 2, pp. 186-197.
11. L. Oudin, A. Kay, V. Andréassian, C. Perrin, “Are Seemingly Physically Similar Catchments Truly Hydrologically Similar?”, Water Resources Research, 2010, vol. 46, no. 11. 15 p.
12. T. Razavi, P. Coulibaly, “Streamflow Prediction in Ungauged Basins: Review of Regionalization Methods”, Journal of hydrologic engineering, 2012, vol. 18, no. 8, pp. 958-975.
13. M. Sivapalan et al., “IAHS Decade on Predictions in Ungauged Basins (PUB), 2003-2012: Shaping an Exciting Future for the Hydrological Sciences”, Hydrological Sciences Journal, 2003, vol. 48, no 6, pp. 857-880.
14. The Global Runoff Data Center, 56068 Koblenz, Germany. www.bafg.de.
15. G. Weedon et al., “The WFDEI Meteorological Forcing Data set: WATCH Forcing Data Methodology Applied to ERA-Interim Reanalysis Data”, Water Resources Research, vol. 50, no. 9, pp. 7505-7514.







