Sevastopol, Russian Federation
BISAC NAT010000 Ecology
BISAC NAT045050 Ecosystems & Habitats / Coastal Regions & Shorelines
BISAC NAT025000 Ecosystems & Habitats / Oceans & Seas
BISAC NAT045030 Ecosystems & Habitats / Polar Regions
BISAC SCI081000 Earth Sciences / Hydrology
BISAC SCI092000 Global Warming & Climate Change
BISAC SCI020000 Life Sciences / Ecology
BISAC SCI039000 Life Sciences / Marine Biology
BISAC SOC053000 Regional Studies
BISAC TEC060000 Marine & Naval
The Black Sea is an enclosed deep marine basin, where the structure of tidal movements is dominated by the direct influence of the tidal force on the proper water body. We investigated the spatial structure of its climatic circulation under the impact of tides. We developed a program module extending the numerical general circulation model of the Black Sea which was designed in the Institute of numerical mathematics, Moscow. It allows the lunar semidiurnal harmonics (M_2) influence to be taken into account explicitly via the discrete analogues of the differential equations of motion. Our work reflects the main results of the numerical experiment on the 4x4 km horizontal grid and 40 vertical σ-levels. It was a one-year model run using the CORE atmospheric climatology forcing. We compared the first and the last weeks of simulation and found out that the characteristics of a tidal mode M2 were established at a very short period of time (7 days), which is the estimate of the model’s energy redistribution time scale. The coastal areas where the tidal impact is substantial (~10 cm) were located mainly at the shallow-shelf inlets highly influenced by the climate change. Validation of the cotidal maps showed the reliability of our model at the climatological time scale. In future we will focus on the baroclinic tidal movements and validation with the Marine Hydrophysical Institute database in order to shed new light on physical and ecological processes at the frontal zone along the Rim Current.
coastal dynamics, numerical modeling, Black Sea, tidal waves.
I. Description of the model
The circulation model of the Black and the Azov Seas was developed at the Institute of numerical mathematics (INM) of the Russian Academy of Sciences (RAS). It is based on a system of primitive equations written in the spherical coordinate system with the approximations of hydrostatics and Boussinesq. The equations of the model are written in the symmetrized form, as follows:



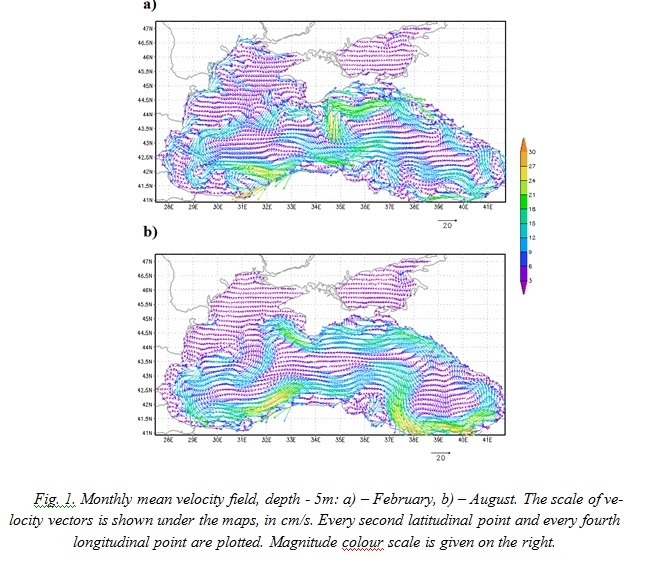
The structure of the circulation agrees well with the existing concept of the circulation patterns in the Black Sea [6]. Two large-scale cyclonic gyres in the eastern and the western parts of the sea are poorly reproduced by the model due to the coarse spatial resolution of the applied atmospheric forcing (Fig. 2).
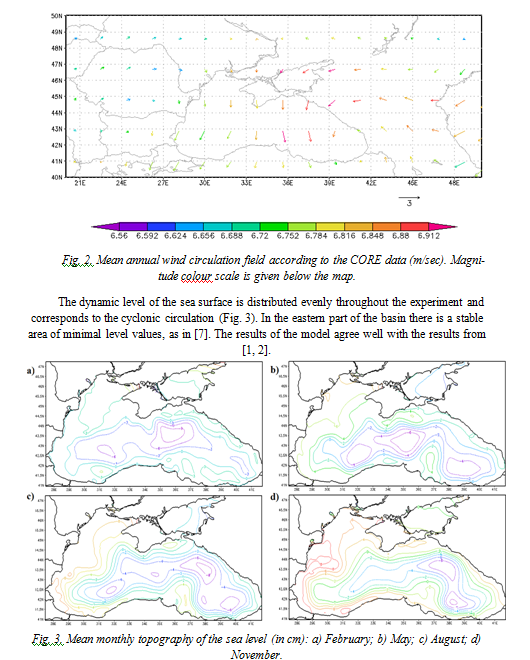
The dynamic level of the sea surface is distributed evenly throughout the experiment and corresponds to the cyclonic circulation (Fig. 3). In the eastern part of the basin there is a stable area of minimal level values, as in [7]. The results of the model agree well with the results from [1, 2].
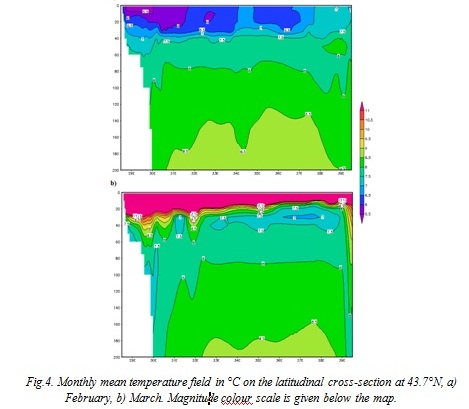
The Cold Intermediate Layer (CIL) is visible at the depths of 40-100 m. It is well reproduced by the model during the all period of the calculation (Fig.4). In February the CIL is renewed and, consequently, it appears at the depths of 0 – 50 m (Fig. 4a). In August (Fig. 4b) the CIL is positioned at the depths of 20 – 80 m, with its core (T<7.5°C) found at 25 – 50 m.
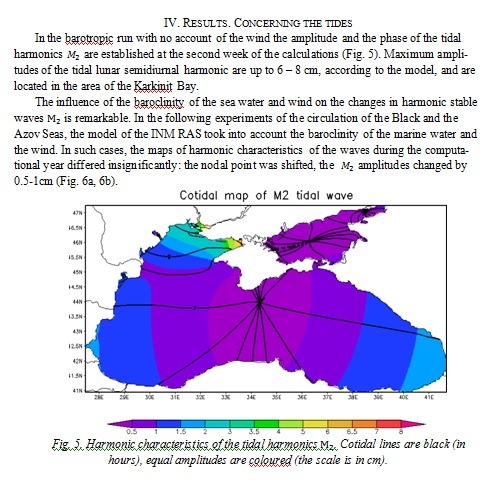
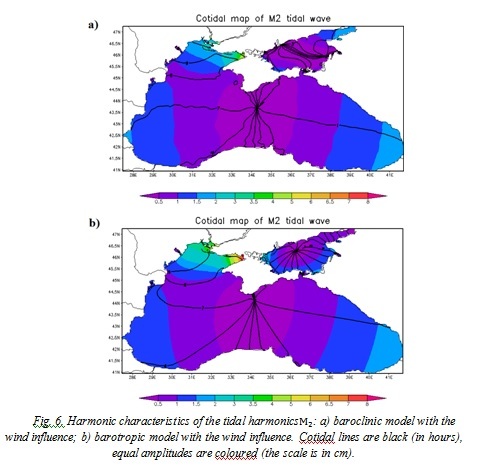
In order to validate the tidal characteristics given by the model, we compare it with the in-situ observations [8, 9]. Field observations analyzed the oscillation spectrum of the Black Sea according to the prolonged sets of studies at 23 stations. The comparison of the amplitudes of the lunar semidiurnal harmonics resulting from the model with the field research showed fine quantitative agreement (table 1).
Table 1. Comparative table of the
|
Location |
Observations data, cm |
Modelling results, cm |
|
Prorva |
0.9-1.7 |
1-1.5 |
|
Odessa |
2-3 |
2-3 |
|
Yalta |
0.1-0.5 |
0-0.5 |
|
Batumi |
2.3-2.8 |
1.5-2 |
Tidal oscillations of the sea level from both sources (field data and data obtained from numerical modelling) are appeared as sharp delta-shaped peaks, corresponding to the frequency of the tidal harmonic
.jpg)
Cotidal maps resulting from the numerical modelling were compared to the theoretical and the field data [9-11] and revealed fine agreement with those.
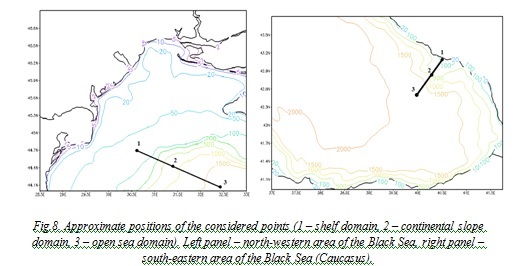
We can notice some peculiarities, which are appeared, when we consider points in different sea domains: shelf, continental slope, open sea. We took these points in north-western and Caucasian areas of the Black Sea on the lines, which are perpendicular to the coast for the each area (fig. 8) and considered their kinetic energy spectra. The spectra were calculated from the data on the kinetic energy oscillations at the depth of main pycnocline (75 m).
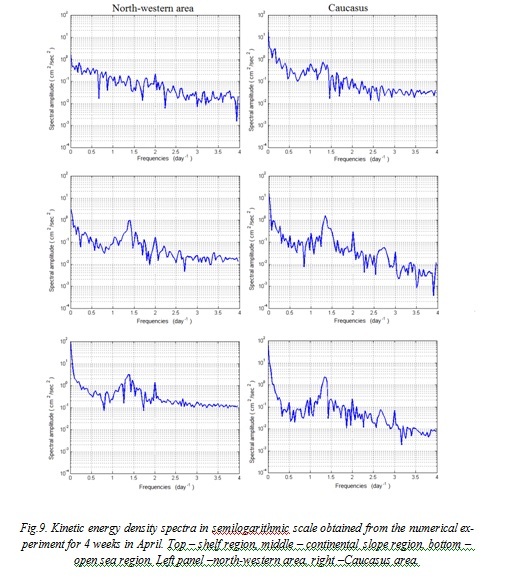
Fig.9 represents the power spectral energy for north-western and Caucasian areas of the Black Sea. These spectra in all points have M2 tidal wave peaks near 2 day-1 frequencies. In the regions of continental slope and open sea well-marked peaks are seen with frequencies close to 1.4 day-1 and energy that sufficiently exceed those of tidal maxima. We assume that these are inertial oscillations of the basin.
The right panel of Fig. 9 corresponds to the area with narrow Caucasian shelf, with two peaks that are absent from the left panel spectra. Their frequencies of 3 and 2.75 day-1 correspond to a baroclinic Poincare wave, previously described in [12] according to the interpretation of in-situ measurements and previous theoretical studies. Such a conclusion is supported by the fact that the peaks are absent from the left panel due to the flatness of the northern-western shelf; they are almost absent from the top-right spectrum due to the location of the sampling point over the shallow area. Presence of those high-frequency baroclinic oscillations over the steep Caucasian shelf demonstrates an important ability of the model to redistribute additional energy generated by the tidal force into the internal waves of a complex nature with properties close to those observed in-situ.
V. Conclusions
The circulation model of the Black and the Azov Seas with account of lunar tidal forces was presented. Model shows good agreement with the coastal long-term measurements and theoretical understandings. Possibilities, which are become available with use of the numerical modelling, allow us to compute tidal influence with higher spatial resolution in relation to the in-situ measurements. First of all, this is actually to the coastal regions.
Furthermore, the model outputs make it possible to investigate the physics of tides and specialties of the energy distribution in different sea regions.
1. V.B. Zalesny, N.A. Diansky, V.V. Fomin, S.N. Moshonkin and S.G. Demyshev “Numerical Model of the Circulation of the Black Sea and the Sea of Azov,”. Russ.J.Numer.Anal. Math. Modelling, № 6, vol. 25, pp. 581-609, 2012.
2. V.B. Zalesny, A.V. Gusev, S.N. Moshonkin, “Numerical Model of the Hydrodynamics of the Black and the Sea of Azov with Variational Initialization of Temperature and Salinity,” Izvestiya. Atmospheric and Oceanic Physics, № 5, vol. 49, pp. 699-716, 2013.
3. G.I. Marchuk, Methods of Computational Mathematics. Saint Petersburg: Lan, 2009. (In Russian).
4. V.I. Agoshkov, M.Y. Assovsky. “A Study of the Tidal Wave M_2 with the Method of Harmonic Analysis Based on Numerical Computation on the Full Model of the Ocean Dynamics,” Moscow, 2010, unpublished. (In Russian).
5. Geophysical Fluid Dynamics Laboratory: http://data1.gfdl.noaa.gov/, last revised on 12.05.2016.
6. V.A. Ivanov, V.N. Belokopytov, Oceanography of the Black Sea. Sevastopol: MHI NASU, 2011. (In Russian).
7. G.K. Korotaev, V.N. Eremeev. Introduction into Operational Oceanography of the Black Sea. Sevastopol: ECOSI - Gidrofizika, 2006. (In Russian).
8. I.P. Medvedev, E.A. Kulikov, A.B. Rabinovich, “Tides in isolated seas: the Baltic, the Black and the Caspian”, in proceeding of “Marine Research and Education: MARESEDU-2015”, 2015. (In Russian).
9. I.P. Medvedev, E.A. Kulikov, “Spectrum of Mesoscale Sea Level Oscillations in the Northern Black Sea: Tides, Seiches, and Inertial Oscillations”, Oceanology, № 1, vol. 56, pp. 10-17, 2016.
10. Defant A. Physical Oceanography, v.2. New York: Pergamon Press, 1961.
11. V.P. Yastreb, T.V. Khmara, “Comparative characteristic of tidal wave motions in seas of the Mediterranean type”, Ecological safety of coastal and shelf zones and complex exploitation of shelf resources, iss. 12, pp. 60-69, 2005. (In Russian).
12. Bagaev A., Ivanov V., Zima V. Statistical analysis of mesoscale variability of the marine environment at the Crimean shelf in summer conducted with in situ data // Ecology, economics and computer science. Coll. Articles: ed. G.G. Matishov et al. V. 2: System analysis and modeling of economic and ecological systems, Southern Federal University, 2015, Pages: 569-580. (In Russian).








