Russian Federation
BISAC NAT010000 Ecology
BISAC NAT045050 Ecosystems & Habitats / Coastal Regions & Shorelines
BISAC NAT025000 Ecosystems & Habitats / Oceans & Seas
BISAC NAT045030 Ecosystems & Habitats / Polar Regions
BISAC SCI081000 Earth Sciences / Hydrology
BISAC SCI092000 Global Warming & Climate Change
BISAC SCI020000 Life Sciences / Ecology
BISAC SCI039000 Life Sciences / Marine Biology
BISAC SOC053000 Regional Studies
BISAC TEC060000 Marine & Naval
Modelling study of the equilibrium profiles formed on sandy coasts of different bed slopes and grain sizes under the various wave conditions was realized by using the CROSS-P and Xbeach morphodynamic models. A special criterion taking into account a total volume of bed deformations per one hour was suggested to determine the conditions of profile stabilization. For both models the time scales of equilibrium profile formation were found to be the same. However, the deformation magnitudes differed significantly. Bed deformations were computed on the whole profile length over the 200-hours duration of wave impact. It was concluded that both models predict a trend of the bed slope toward a stable value. CROSS-P model shows the widening of accumulative terrace during the profile evolution. The mean slope of the equilibrium profile was found to depend on the initial bed slope.
equilibrium beach profile, cross-shore sediment transport, bed deformations.
Impact of sea waves on a sandy coast excites the bed deformations in order to adjust the coastal profile to a given wave impact. In case of stable wave regime during a sufficiently long time, coastal profile reaches an equilibrium condition. According to experiments in wave flume [1], bed deformations more significant at the beginning and gradually decrease further (fig.1). In some cases absolute volume change stable increases and it proved that equilibrium profile doesn’t exist. Investigations of forming of equilibrium beach profile is not allow to estimate time of adjusting of bed relief to wave impact and volume of corresponding bed deformations [1,2].
There is a necessity of investigation of forming of equilibrium beach profile and stabilization of coastal relief under steady wave impact. It helps to solve any fundamental problems of coastal lythodynamics, especially estimation of bed deformation due to storm with different duration and intensity storm phases. Moreover on artificial coasts, profiles during construction are generally much steeper than nature profiles. Estimation of non-equilibrium beach profile reshaping increases efficiency of beach nourishment actions.
II. Methods
Investigation was conducted by lithodynamic simulating in models CROSS-P and Xbeach. Both models simulate coastal profile response in particular to extreme storm events. СROSS-P model based on the equation of mass conservation that relates bed deformations with gradients of cross shore sediment transport [3]. Module of sediment transport based on Bagnold’s energy concept that determines dependence between quantities of moved sediments anв energy dissipation speed. Хbeach model is an open source program and based on solver of coupled 2D equations for wave propagation, flow, sediment transport and bottom changes for varying wave and flow conditions. A detailed description of the model can be found in Roelvink et al., 2009 [4].
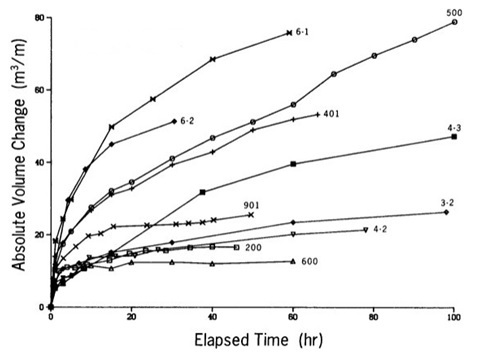
Fig 1. Absolut sum of profile change according results physical experiments in wave flume [1].
Investigation consists of two parts. First part includes investigation in relation to quasi-equilibrium condition of beach profile with special criterion that was defined by volume of deformations per hour about 5% of summarizes deformations. Second part consists of research evolution of profile under the unreal long wave impact for proof of existing of stabilization of profile that defined by absolute bed deformations.
Previously [5] proposed index for evaluating bed deformations:

Second part of investigation based on simulation unreal long storm impact and includes:
- comparison of shape of resulting profiles that predicts by different models;
- distribution on profile and estimation of values of bed deformations per hour during storm impact;
- estimation of shape of equilibrium profile that generates on different initial slopes, but with the same geological conditions (sediment size) and equivalent wave regimes.
III. Results
Quasi-equilibrium condition of beach profile
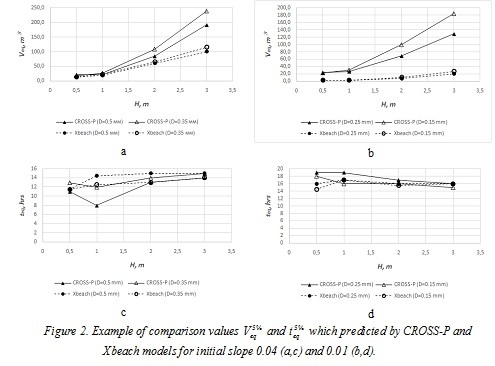
Numerical modeling allows to define parameters of nearly stable beach profile (deformation per hour 5% of total deformations). Determined that necessary time for forming quasi-equilibrium profile (teq5%) close to duration of stabilization phase of real storms (12-20 hours, fig 2c and 2d). It’s time decreases for steeper initial slope. Values of total deformations for nearly stable profile (V5%eq) increases for steeper slopes (fig 2a and 2b), more intensive wave impact and reducing of sediment grain size. Comparison of results of different models revealed that Xbeach predicted volume deformations of coastal relief (V5%eq )make-up 60 percent of values that predicted be CROSS-P model.
Equilibrium in relation to absolute bed deformations
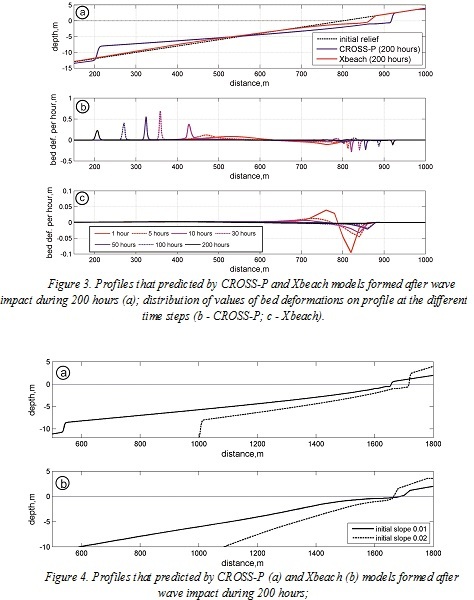
It should be noted that both models predict different shape of profile and different intensity of deformations under wave impact with the same wave parameters.(fig 3a). CROSS-P model in relation to Xbeach model predicts deeper profile, wider accumulative terrace and more significant retrogradation of coastline. For both models deformation during first hours of wave impact occurs on full length of profile (fig 3b and 3c). Slope of profile becomes stabilize after 5-10 hours of wave impact for CROSS-P model and after 10 hours for Xbeach model. CROSS-P model predicts widening of accumulative terrace after stabilization of profile slope. This process is defined by cross shore sediment transport and accompanied by erosion on land side and accumulation on seaside. Intensity of widening of profile is decay during wave impact. On example of slope 0.02 (d=0.25 mm, H=3 m, T=7 s) was offered that after 10 hours of wave impact front of accumulative terrace moves forward with speed 3.5 m per hour. This speed decreases after 100 hours till 0.6 m per hour.
It follows from both models that on steeper initial bed slope a steeper resulting profile arises. However, the final results for the same initial conditions are different. For sand size 0.25 mm and initial slopes 0.01 and 0.02 the CROSS-P model predicts the quasi-equilibrium profiles with the mean slopes 0.007 and 0.012, respectively, while the Xbeach model predicts the mean slopes 0.004 and 0.013.
III. Conclusion
Study performed highlights the connection of the initial bed morphology and wave conditions with the temporal scale of morphological changes responsible for the equilibrium coastal profile formation.
- Numerical modeling shows that increase in absolute volume of bed deformations V decelerates with the time. Suggested criterion of the equilibrium profile is based on condition that the changes in quantity of V do not exceed 5% per 1 hour.
- Time of forming quasi-equilibrium profile is the same for both models and decreases for steeper initial slope. It was stated that necessary time for forming quasi-equilibrium profile (teq5%) may by comparable with the duration of maximal phase of the real storms (12-20 hours).
- Total volumes of deformations for quasi-equilibrium profile (V5%eq) increases for steeper slopes, more intensive wave impact and reducing of sediment grain size.
- Both models predict different shapes of equilibrium profile and different magnitudes of bed deformations under the same wave impact.
- Both models show that bed deformations during the first hours of wave impact occur over the whole length of the profile. After stabilization of profile, CROSS-P model predicts widening of accumulative terrace with decaying rate.
- Final profiles formed by the same long-time wave impact are not the same for different initial slopes.
IV. Acknowledgment (if needed)
This work was supported by the project №15-05-008239 of Russian Foundation for Basic Research and financial support of theme defined in Government Task №0149-2014-0034.
1. Larson M., Kraus N.C. SBEACH: numerical model for simulating storm-induced beach change. Tech. Rep. CERC-89-9. 1989. US Army Eng. Waterw. Exp. Station. Coastal Eng. Res. Center.
2. Leontiev I.O. Coastal dynamics: waves, currents and sediments drifts. Moscow.: GEOS, 2001. pp. 272.
3. Leontiev I.O. Morphodynamic processes in coastal zone. LAP LAMBERT Academic Publishing, 2014. pp. 251.
4. Roelvink, D., Renier, A., Van Dongeren, A., Van Thiel de Vries, J., McCall, R., Lescinski, J., 2009. Modeling storm impacts on beaches, dunes and barrier islands. Coastal Engineering. Amsterdam: Elsevier Science Publishers. v. 56. p. 1133-1152.







